Atcoder Series

abc392 F

Link:https://atcoder.jp/contests/abc392/tasks/abc392_f

Analyse

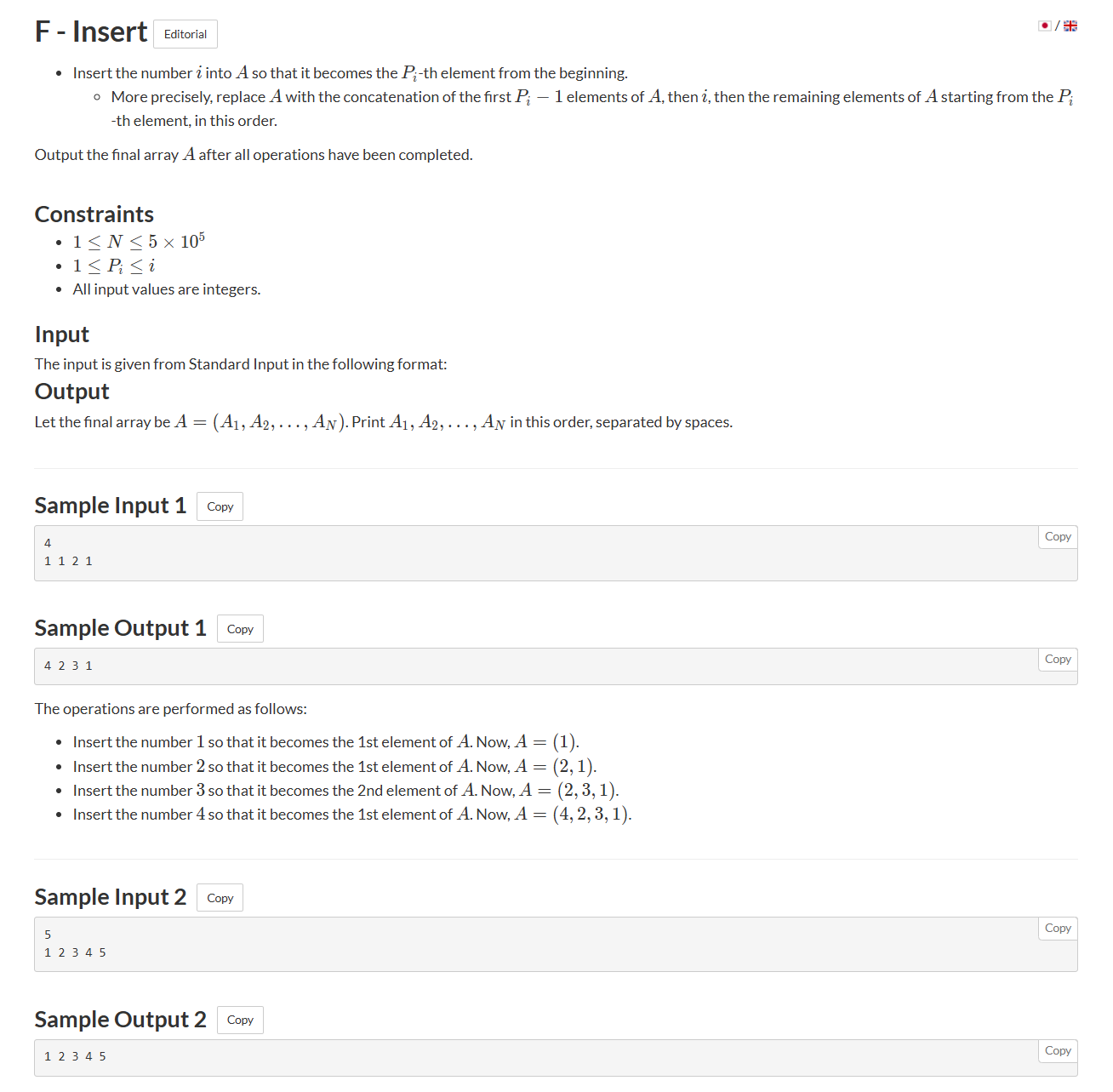
一开始有n个值, 这n个值从左到右排成1-n的序列, 从后往前遍历, 数字n在序列中的下标为a[n], 数字n的位置首先被确定, 然后将该序列中下标为a[n]的值删掉, 序列长度变为n-1, 数字n-1在剩余序列中的下标为a[n-1], 得出数字n-1的位置, 依此类推，最终得出数字1-n的所有位置。
这个过程可以用树状数组模拟, 初始数组1-n下标的值都为1, 从后往前每遍历一个就删掉一个被确定的位置, 然后二分最大的前缀和小于等于a[i]的下标或者最小的前缀和大于等于a[i]的下标, 二分得出的下标即为该数字的位置

Code

#include <bits/stdc++.h>
#define lowbit(x) x & -x
using namespace std;
const int N = 5e5 + 10;
int f[N], n;

void add(int x, int v) {
    for (int i = x; i <= n; i += lowbit(i))
        f[i] += v;
}

int get(int x) {
    int sum = 0;
    for (int i = x; i; i -= lowbit(i))
        sum += f[i];
    return sum;
}

void solve() {
    cin >> n;
    vector<int> a(n + 1);
    for (int i = 1; i <= n; i++) {
        add(i, 1);
        cin >> a[i];
    }
    vector<int> res(n + 1);
    for (int i = n; i >= 1; i--) {
        int l = 1, r = n;
        while (l < r) {
            int mid = (l + r) / 2;
            if (get(mid) >= a[i])
                r = mid;
            else
                l = mid + 1;
        }
        res[l] = i;
        add(l, -1);
    }
    for (int i = 1; i <= n; i++)
        cout << res[i] << " \n"[i == n];
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

abc393 E

Link:https://atcoder.jp/contests/abc393/tasks/abc393_e

Analyse

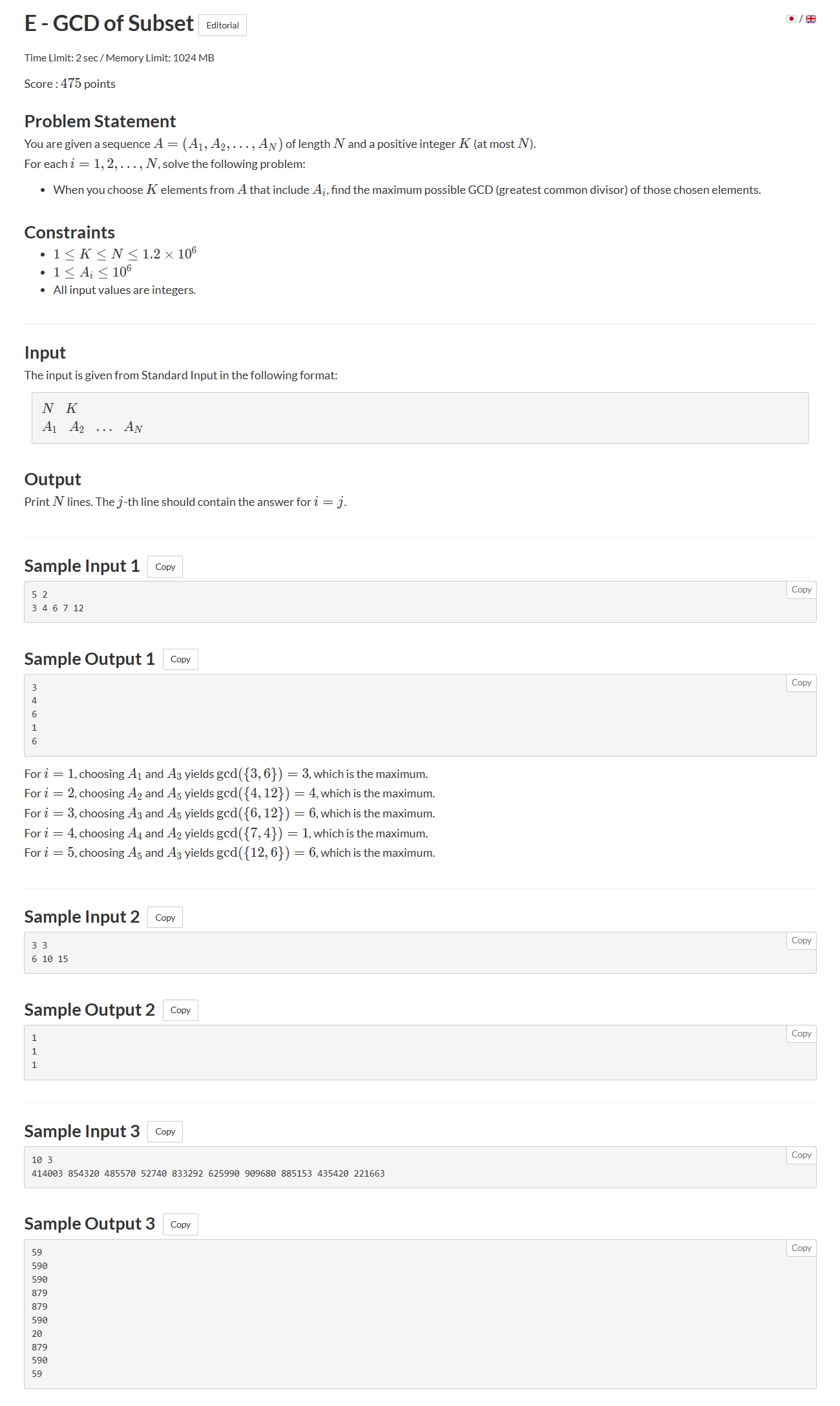
首先对数组进行计数，然后枚举gcd，计算原数组有多少个数是该gcd的倍数，若大于等于k，则更新答案
时间复杂度

时间复杂度是O(n log n)

Code

#include <bits/stdc++.h>
#define lowbit(x) x & -x
using namespace std;
const int N = 5e5 + 10;

void solve() {
    int n, k;
    cin >> n >> k;
    vector<int> cnt(1000000 + 10);
    vector<int> a(n);
    for (int i = 0; i < n; i++) {
        cin >> a[i];
        cnt[a[i]]++;
    }
    int mx = 1e6;
    vector<int> res(mx + 1);
    for (int i = 1; i <= mx; i++) {
        int c = 0;
        for (int j = i; j <= mx; j += i)
            c += cnt[j];
        if (c >= k) {
            for (int j = i; j <= mx; j += i) {
                res[j] = max(res[j], i);
            }
        }
    }
    for (int i = 0; i < n; i++)
        cout << res[a[i]] << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

abc391 F

Link:https://atcoder.jp/contests/abc391/tasks/abc391_f

Analyse

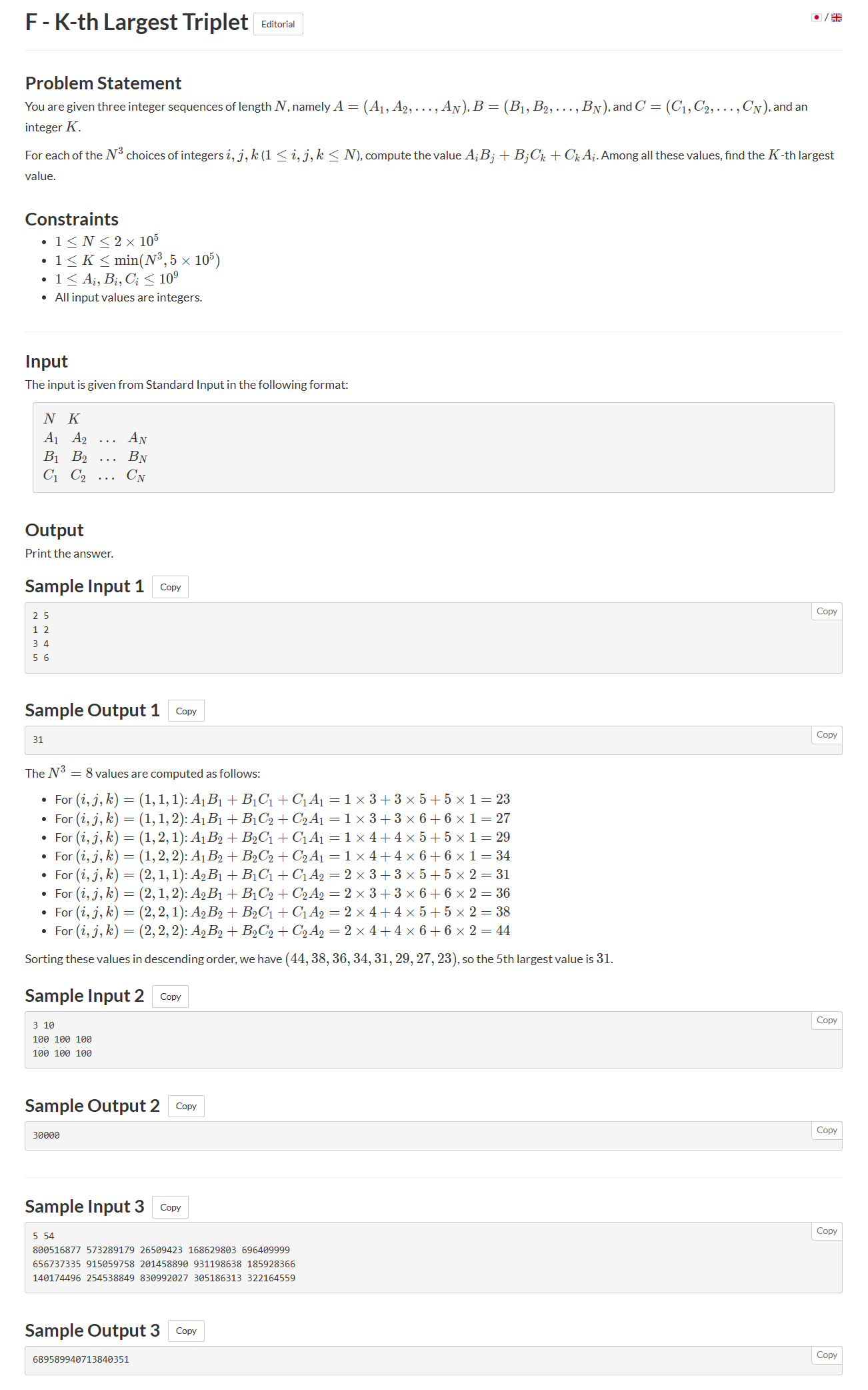
先对三个数组从大到小排序
使用优先队列进行BFS，先将最大值和三个数组对应的下标放进堆，然后依次对(i+1, j, k)，(i, j+1, k)，(i, j, k+1)进行扩展，因为是大根堆，所以第k次取出的一定是第k大的，后面的因为下标增加，而数组又是从大到小排序，所以一定小于等于第k次取出的值

Code

#include <bits/stdc++.h>
#define lowbit(x) x & -x
using namespace std;
const int N = 5e5 + 10;

void solve() {
    int n, k;
    cin >> n >> k;
    vector<int> a(n), b(n), c(n);
    for (int i = 0; i < n; i++)
        cin >> a[i];
    for (int i = 0; i < n; i++)
        cin >> b[i];
    for (int i = 0; i < n; i++)
        cin >> c[i];
    sort(a.begin(), a.end(), greater());
    sort(b.begin(), b.end(), greater());
    sort(c.begin(), c.end(), greater());
    map<vector<int>, bool> vis;
    priority_queue<array<long long, 4>> pq;
    long long res;
    auto cal = [&](int i, int j, int k) -> long long {
        return 1ll * a[i] * b[j] + 1ll * b[j] * c[k] + 1ll * a[i] * c[k];
    };
    pq.push({cal(0, 0, 0), 0, 0, 0});
    vis[{0, 0, 0}] = true;
    while (k--) {
        auto t = pq.top();
        long long val = t[0];
        int i = t[1], j = t[2], k = t[3];
        pq.pop();
        res = val;
        if (i + 1 < n) {
            vector<int> v = {i + 1, j, k};
            if (!vis[v]) {
                vis[v] = true;
                pq.push({cal(i + 1, j, k), i + 1, j, k});
            }
        }
        if (j + 1 < n) {
            vector<int> v = {i, j + 1, k};
            if (!vis[v]) {
                vis[v] = true;
                pq.push({cal(i, j + 1, k), i, j + 1, k});
            }
        }
        if (k + 1 < n) {
            vector<int> v = {i, j, k + 1};
            if (!vis[v]) {
                vis[v] = true;
                pq.push({cal(i, j, k + 1), i, j, k + 1});
            }
        }
    }
    cout << res << "\n";
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    // cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}

Atcoder Series